GA091 Berlín, 4 de noviembre de 1904 - Trigonometría

  Índice

 RUDOLF STEINER. 

NOTAS DE MATHILDE SHOLL 1904 - 1906   

TRIGONOMETRÍA

 Berlín, 4 de noviembre de 1904

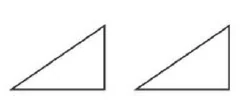
Los triángulos que pueden superponerse exactamente uno encima del otro se llaman congruentes. Si no pueden superponerse exactamente una sobre otra, pero sí pueden superponerse de tal manera que una pueda colocarse encima de la otra, aunque no del mismo tamaño, se consideran similares si las terceras líneas son paralelas y se solapan parcialmente.

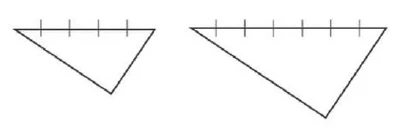
Una cara de cinco unidades de largo. Un lado de siete unidades de largo.

Para conseguir un triángulo similar, conecto el tercer punto y el quinto, y luego obtengo dos líneas paralelas.

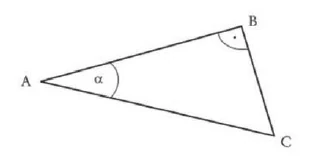
Dos triángulos son similares si pueden superponerse uno sobre otro, coincidiendo en un ángulo y con dos lados paralelos.

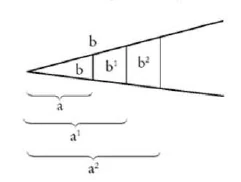
Dos triángulos son similares si tienen los mismos ángulos. En triángulos similares, los lados opuestos al mismo ángulo tienen las mismas proporciones.

es una proporción

Si multiplicas los dos términos externos o los dos términos internos, obtienes el mismo producto: Entonces .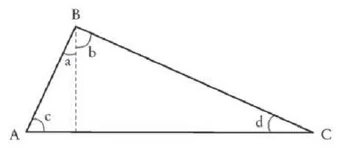

El cuadrado de la perpendicular es igual al producto de las dos partes de la hipotenusa.

Lemniscate (multiplicación)

Círculo (División)

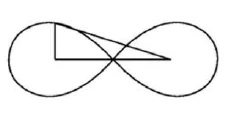
Puedes cruzar el diámetro en la circunferencia tres veces y entonces queda un resto, que es aproximadamente  del diámetro. Así que la circunferencia del círculo es  multiplicado por el diámetro.

GA091 Berlín, 9 de noviembre de 1904 - Seno, Coseno, Tangente, Cotangente

 Índice

 RUDOLF STEINER. 

NOTAS DE MATHILDE SHOLL 1904 - 1906   

SENO, COSENO, TANGENTE, COTANGENTE

 Berlín, 9 de noviembre de 1904

Puedes trazar el ángulo Alfa un grado.

\(BC:AC\) – La razón \(BC:AC\) es la razón del ángulo Alfa. La proporción se llama pecado. (Sino) del ángulo. (\(AC:AB =\) coseno de Alfa)
\(BC:AC = \sin(\alpha)\)
\(AB:AC = \cos(\alpha)\)
\(BC:AB \tan(\alpha) = tg \alpha\)(\(BC:AB = \)tangente \(a\))
\(AB:BC \cot(\alpha)\) (\(AB:BC =\) cotangente \(a\))

Puedes determinar una línea torcida en un plano calculando las distancias entre ella y dos rectas. Este método se utilizó por primera vez en los últimos siglos, por Cartesius. Este método se denomina geometría analítica.

---

\(x^2 + y^2 = r^2 =\) la ecuación del círculo.

Al determinar la legalidad de la distancia en un sistema particular de líneas que se cruzan, se obtiene el círculo.

(0\) es el centro del sistema de ejes de coordenadas. Los antiguos (Ptolomeo) asumieron el centro de la tierra, pero Copérnico asumió el sol. Lo relacionaba todo con el Sol. Sin embargo, aún tuvo en cuenta que la Tierra tiene su propio movimiento además de su movimiento alrededor del Sol, y que este movimiento es similar al movimiento de la Tierra alrededor del Sol. En las escuelas, la tercera frase de Copérnico suele omitirse. En el sistema copernicano, la Tierra en realidad se mueve en una trayectoria helicoidal (Vara de Hermes).

El sistema de Ptolomeo se basaba en el plan astral. El descubrimiento de Copérnico significaba que el movimiento relativo del sistema planetario se basaba en un punto de origen diferente (el punto físico de origen).

En la Divina Comedia de Dante, todo se basa en el plan astral; la Tierra es el centro.

En el ángulo se puede ver la curvatura de la línea. El matemático determina el ángulo según la tangente. Con cada nueva distancia, la tangente cambia, mayor o pequeña.

Tan A es absolutamente variable respecto a la curva a distancias muy pequeñas. Entonces tan a se llama cociente diferencial. Se pasa de cantidades finitas a cantidades infinitamente pequeñas. Newton también lo llamó cálculo de flexión (cálculo del movimiento). Leibniz hizo el descubrimiento al mismo tiempo. Era necesario encontrar el infinito en el propio plano físico.

\(\tan(\alpha) = \frac{x}{y}\) (si \(a\) y \(b\) son variables)

Dos líneas que van al infinito, entre ellas un área infinitamente grande.

Fl. \((ab) = \infty\) (infinitamente grande)
Fl. \(ac)= \infty =2 \infty\)
(Dividir un infinito por otro da \(2\))
\(\frac{\infty}{\infty} = 2\)

Una línea recta infinita es un círculo. Sin embargo, esto no es posible en el espacio tridimensional porque tomaría un tiempo infinito. Si no es un espacio tridimensional sino bidimensional, entonces es diferente. Entonces el tiempo mismo es la cuarta dimensión. Entonces no solo se produce un movimiento en esa dirección, sino también otro cambio. Supongamos que te mueves en una dirección (una bola que se hace cada vez más grande). Luego, cuando la bola alcanza cierto tamaño, será posible que diverga hacia el otro lado. Pero entonces debía haber fuerzas que lo mantenían unido. En el espacio astral, se añade el efecto como cuarta dimensión.